
Review of background and recent results
Quantum decoder and related technologies
Recent progress of quantum communication theory clarifies the ultimate limit of communication with electromagnetic fields through a linear-loss channel, and also a scheme to approach to the limit. In Fig. 1, we compare predicted performances of quantum and optical communications, from the viewpoint of how the channel capacity scales as a function of the launch power. The performance of a near future optical communication for a single fiber is forecasted by using the Shannon formula
Here P is the launch power, i.e. an input power into the transmitter side of a fiber, W is a bandwidth of the channel, N is an average noise power for the whole bandwidth, and η is an effective transmissivity of the signals from the fiber input to the output via the amplifiers. A recent experiment by Alcatel-Lucent [G. Charlet, et al. Transmission of 16.4Tbits/s Capacity over 2,550km using PDM QPSK Modulation Format and Coherent Receiver. In OFC/NFOEC 2008. San Diego, USA.], employed the c-band of 2THz, and attained roughly a signal-to-noise ratio (SNR) of 20 dB for the launch power of P = 1W, whose performance is marked by the red circle in Fig. 1. We may then roughly assume η~10-2 and N~100μW. The performance of near future optical communication is obtained by extending the bandwidth to the whole available one W = 50THz with a commercial fiber, corresponding to the wavelength range of about 1.2-1.6μm, and also assuming an advanced technology of multi-ary modulation of light-wave signals and phase-sensitive detection of the signals.
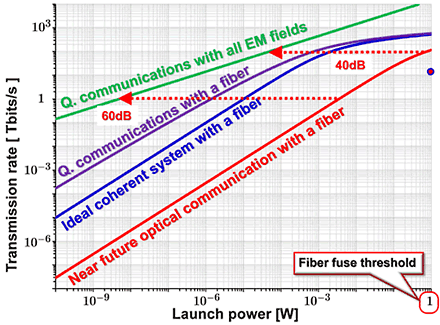
Fig. 1Channel capacities of quantum and optical communications.
This level of technology still suffers from amplified spontaneous emission noise in an amplifier, and the excess noise in a detector. To reduce these excess noises, we have to realize quantum optimal amplifiers and excess-noise free homodyne detectors. We could then expect ideal coherent communications where only the quantum noises dominate. Its performance is shown by the blue curve in Fig. 1.
Quantum mechanically there is a better scheme. In this context, given a lossy channel, and the power and bandwidth constraints, one could do anything allowed by quantum mechanics to transmit the maximum information. Thus the ultimate capacity must be derived by fully quantum mechanical optimization of encoding and decoding strategies. The solution of this difficult problem has recently been solved [V. Giovannetti, et al., Classical capacity of the lossy bosonic channel: The exact solution. Phys. Rev. Lett. 92, 027902, (2004)]. The theory can be applied to the case of a fiber with a 50THz bandwidth. Its performance is shown by the purple curve in Fig. 1. When the bandwidth constraint is removed, assuming a new transmission material, then we the ultimate capacity of a bosonic channel with all electromagnetic field modes. This limit is given by the formula
which is shown by the green curve. Nobody can go beyond this limit no matter how much capacity we want. Thus quantum information theory tells us that the capacity is finite. The very origin of this is the inevitable quantum noise, as represented by the uncertainty relation ΔxΔp ≥ h = 6.6×10-34 J·s, where h is the Plank constant, and x and p are the quadrature amplitude and phase of an optical field.
Importantly, this theory tells us, not only the capacity formula, but also what the optimal scheme looks like. The optimal encoding is given by the coherent modulation, which is completely conventional technology. The optimal decoding, on the other hand, essentially requires quantum effect. This should consist of quantum computing with coherent states to transform the received codeword state into an appropriate quantum state, and the final measurement on it afterward. This is called quantum collective decoding. See Fig. 2.
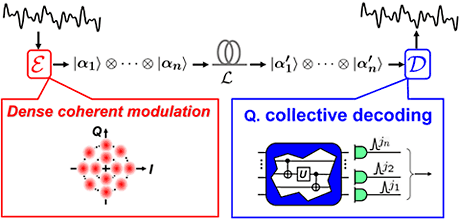
Fig. 2Optimal transmission scheme for a lossy optical channel.
The quantum gain in the capacities originates from the quantum interference in the detection process. In Fig. 3, classical and quantum detection schemes are compared. In classical scheme, the channel matrix is given. We do not ask further detailed structure of probability. In the quantum scheme, however, the channel matrix is the absolute square of quantum probability amplitude. It is an inner product between the measurement vector |my> and the signal state vector |x>, as P(y|x) = |<my|x>|2. Thus in the quantum domain, there exists a lower level layer in the channel matrix, and we can control this probability amplitude directly to induce an appropriate quantum interference for a better SNR.
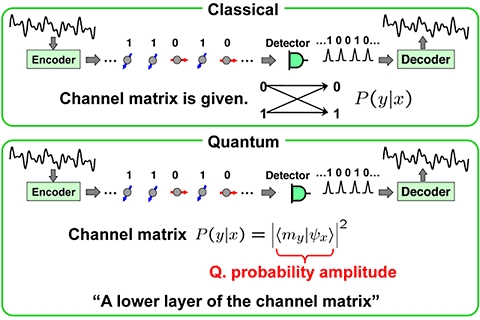
Fig. 3Channel matrix and quantum probability amplitude.
This direct control of quantum probability amplitude in the detection process brings a new remarkable effect, when we consider the coding. It is the super-additive coding gain. This can be summarized in the following way (See Fig. 4). When we increases the transmission resources by n times, then the capacity can increase even more than n times. Classically, however, the capacity increases n times at most, and never more than that.
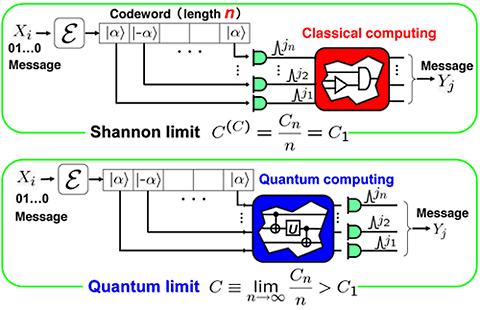
Fig. 4Comparison of quantum and classical decoding schemes.
The very origin of this effect is quantum computing, which is performed prior to the measurement. An example of length 2 coding is schematically shown in Fig. 5. We first transform the received pulses into a superposition of several possible sequences by a quantum computer, and then perform a measurement afterward. In the measurement process, these probability amplitudes interfere with each other, reducing the decoding error. In the classical scheme, in contrast, each pulse is first measured separately, producing all possible sequences. They are then decoded by classical processing. In that case, the channel matrix element is simply the product of these two, and the capacity is just additive. The important principle of super-additive coding gain was demonstrated in 2003 by NICT. In the experiments, single photon states in the polarization-location coding were used [M. Fujiwara, et al., Phys. Rev. Lett., 90,167906 (2003)]. But this coding scheme is just a toy model for proof-of-principle demonstration. In practice, the super-additive coding gain should be realized with coherent states. It is actually a very difficult task. Currently only parts of basic elements are implemented, such as quantum receiver, and quantum signal processing with continuous variable states. The proof-of-principle demonstration of quantum decoder with coherent states is a challenge in this decade.
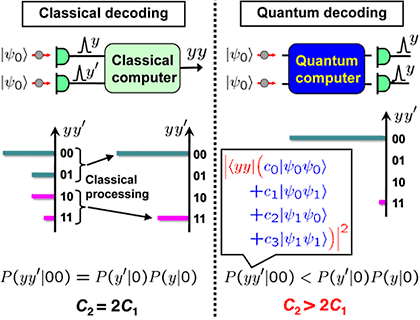
Fig. 5Quantum and classical decoding in the case of length two coding. The quantum interference at the probability amplitudes reduces the decoding error.
Even small scale quantum decoder would be useful, when combined with a classical decoder to reduce the decoding complexity, and boost the effective transmission performance [M. Takeoka, et al. Phys. Rev. A, 69, 052329 (2004)]. The quantum capacity limits in Fig. 1 is attained when a large scale quantum decoder is implemented, which is a grand challenge in this century. Quantum decoder will also be indispensable for deep space optical communications. It is very long distance, but there are no amplifiers. The power feed is very limited. This is a really quantum-limited channel. Quantum theory tells us that, we will be able to extend a Tbps link to Mars from Earth, as seen in Fig. 6.
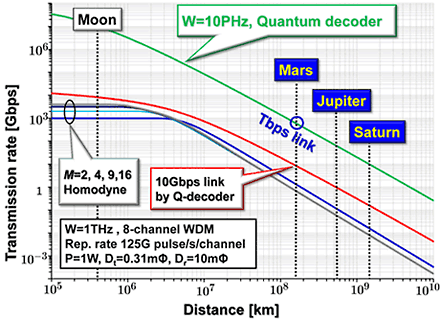
Fig. 6Predictions on the capacities for deep space optical communications.